XII
Зимний турнир Архимеда
Центр образования №109
19.01.2003
Условия
1. Пример на сложение. На
восьми карточках записаны цифры и знаки “плюс” и “равно”: 
, 
, 
, 
, 
, 
, 
, 
. Составьте верный
пример на сложение, используя все указанные карточки.
2. Катер. Имея полный бак топлива,
катер может проплыть 72 км против течения реки или 120 км по течению. На какое
наибольшее расстояние по реке он может отплыть при условии, что топлива должно
хватить и на обратный путь?
3. Четырнадцать ребят: 7 мальчиков и 7 девочек решили
разделиться на две команды. Они встали в круг и начали считаться (по часовой
стрелке). Каждый шестой – выходил из круга, и счет начинался заново со следующего
игрока. Так продолжалось до тех пор, пока 7 вышедших из круга игроков не
образовали команду, причем оказалось, что она состоит из одних мальчиков.
Изобразите схематически, как могли бы стоять мальчики и девочки (не забудьте
указать, с кого начинался счет).
4. Ледяная пустыня. Путешественник хочет пересечь арктическую пустыню
за 6 дней. Известно, что один человек способен взять с собой припасов на 4 дня.
Он не сможет преодолеть весь путь в одиночку, но он может взять с собой
носильщиков. Сколько человек он должен взять с собой и как организовать
путешествие, чтобы благополучно пересечь пустыню, а все носильщики вернулись
домой?
|
5. Клетки марсианского организма “А–2003” расположены в виде замкнутых
“цепочек” и могут находиться в двух состояниях – “сон” и “активность”.
“Активная” клетка раз в секунду передает сигнал, который за секунду доходит
до двух соседних клеток. В следующую секунду клетка “активна”, если к ней
пришел сигнал от одной из соседних клеток.
|
рис.1
|
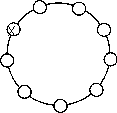
рис.2
|
Если же сигнал пришел с
двух сторон или не пришел вовсе, то клетка погружается в “сон”. Известно, что организм “А–2003”
живет до тех пор, пока хотя бы одна его клетка “активна”. Сколько секунд
проживет организм, изображенный
а) на рис. 1? б) на рис. 2? (“активные” клетки помечены знаком X).
6. Числа на
ребрах куба.
а) Можно ли из чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12, 13 вычеркнуть какое-нибудь одно число, а оставшиеся расставить на
ребрах куба (см. рис.) так, чтобы сумма чисел на трех ребрах примыкающих
к каждой вершине куба была одной и той же?
б) Может ли этим
вычеркнутым числом быть число 13?
