II Зимний турнир Архимеда

Школа №5

24.01.1993

Условия

1. Делимость на 1993. Докажите, что сумма  делится на 1993.

2. На одной ферме число коров на 12,5% меньше, чем на другой, но средний удой каждой коровы на 8% выше. На какой ферме получают молока меньше и на сколько процентов?

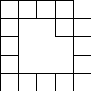
3. Цепочка из плиток. Можно ли сложить замкнутую цепочку из 1993 квадратных плиток? Пример замкнутой цепочки:

4. Верно ли равенство:

?

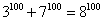5. Фальшивая монета. Среди 12 монет имеется одна фальшивая. Известно, что фальшивая монета отличается от настоящих, но неизвестно легче она настоящей или тяжелее. Все настоящие монеты имеют одинаковую массу. С помощью трех взвешиваний на чашечных весах без гирь выделить фальшивую монету и одновременно установить, легче она или тяжелее остальных.

6. На острове Рыцарей и Лжецов. Перед нами 3 островитянина A, B и C, о каждом из которых известно, что он либо рыцарь, либо лжец. Пусть A и B высказывают следующие утверждения: A: ”Мы все лжецы”, B: ”Ровно один из нас лжец”. Можно ли определить, кто такой B: рыцарь или лжец? Можно ли определить, кто такой C?