XII Турнир Архимеда

Заочный тур

2002/2003 уч. год

Условия

1. В заповедном лесу растут ели, сосны и пихты. Известно, что елей на 20% больше, чем сосен и на 25% больше, чем пихт. Известно, что пихт на 144 меньше чем сосен. Сколько в заповедном лесу елей?

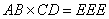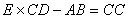2. Буквы вместо цифр. Если , а , то чему равно ?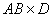

3. Двойки и нули. Число , десятичная запись которого состоит из n двоек, делится на 2002. При каком наименьшем n это возможно? Сколько таких чисел существует?

4. Загадочное пятизначное число. Известно, что в пятизначном числе все цифры различны и не равны некоторой цифре Х. Если записать цифры числа в обратном порядке, то результат окажется меньше исходного числа в Х раз. Найдите это число.

5. В Ледяном дворце Снежной Королевы стояло 6 елок, каждые две из которых были соединены гирляндой из цветной бумаги (белой, красной, зеленой, желтой или синей). Могло ли так быть, чтобы от каждой елки “выходили” гирлянды каждого из 5 цветов?

6.  Продолжение предыдущей задачи. Если бы елок было 13, а цветов 12, могло ли так быть, чтобы от каждой елки “выходили” гирлянды каждого из 12 цветов?

7. Кот Матроскин и почтальон Печкин были в гостях у дяди Федора и теперь возвращаются в Простоквашино. Им надо преодолеть расстояние в 10 км, но на двоих у них имеется один велосипед, без багажника и верхней продольной трубы, так что ехать на нем может кто-то один. Хорошо, что путь проходит по лесной до­роге, на которой в это время суток ни души. Поэ­тому ради справедливости они решили так: один из них едет на велосипеде, через какое-то время слезает, ставит велосипед у дерева и продолжает путь пешком. Второй, шедший пешком, доходит до велоси­педа и садится на него, и так далее. Известно, что на велосипеде они могут ехать со скоростью 10 км/ч, пешком Печкин ходит со скоростью 4 км/ч, а Кот –  5 км/ч. За какое время они смогут вернуться домой?

8. Перепись населения. На острове живет несколько семей с детьми. Вот что известно о населении этого острова.

Детей на острове больше, чем взрослых. Взрослых больше, чем мальчиков. Мальчиков больше чем девочек, а девочек больше, чем семей. Бездетных семей нет, а во всех семьях количество детей разное.

У каждой девочки есть по меньшей мере один брат и не больше одной сестры. В одной из семей детей больше, чем во всех остальных вместе взятых. Сколько семей на острове? Сколько мальчиков и девочек в каждой из семей?